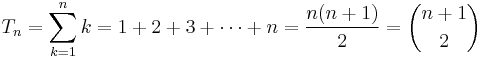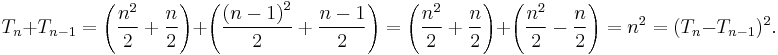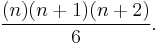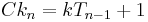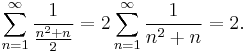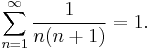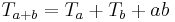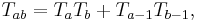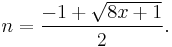Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n. The sequence of triangular numbers (sequence A000217 in OEIS) is:
The triangle numbers are given by the following explicit formulas:
The rightmost expression, consisting of "n + 1" and "2" within parentheses, is a binomial coefficient. It represents the number of distinct pairs that can be selected from n + 1 objects, and it is read aloud as "n plus one choose two". In this form, the triangular number Tn solves the handshake problem of counting the number of handshakes if each person in a room full of n + 1 total people shakes hands once with each other person.
Triangle numbers are the additive analog of the factorials, which are the products of integers from 1 to n.
The number of lines you can draw between each of the dots can be represented with the following recurrence relation:
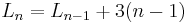
The ratio between the two numbers, dots and lines also has the interesting property of:
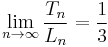
Contents |
Relations to other figurate numbers
Triangular numbers have a wide variety of relations to other figurate numbers.
Most simply, the sum of two consecutive triangular numbers is a square number, with the sum being the square of the difference between the two. Algebraically,
Alternatively, the same fact can be demonstrated graphically:
| 6 + 10 = 16 | 10 + 15 = 25 |
There are infinitely many triangular numbers that are also square numbers; e.g., 1, 36. Some of them can be generated by a simple recursive formula:
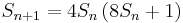 with
with 
All square triangular numbers are found from the recursion
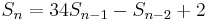 with
with 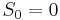 and
and 
Also, the square of the nth triangular number is the same as the sum of the cubes of the integers 1 to n.
The sum of the all triangular numbers up to the nth triangular number is the nth tetrahedral number,
More generally, the difference between the nth m-gonal number and the nth (m + 1)-gonal number is the (n - 1)th triangular number. For example, the sixth heptagonal number (81) minus the sixth hexagonal number (66) equals the fifth triangular number, 15. Every other triangular number is a hexagonal number. Knowing the triangular numbers, one can reckon any centered polygonal number: the nth centered k-gonal number is obtained by the formula
where T is a triangular number.
The positive difference of two triangular numbers is a trapezoidal number.
Other properties
Triangular numbers correspond to the 1st-order case of Faulhaber's formula.
Every even perfect number is triangular, given by the formula
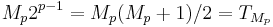
- where Mp is a Mersenne prime. No odd perfect numbers are known, hence all known perfect numbers are triangular.
- For example, the 3rd triangular number is 3x2 = 6; the 7th is 7x4 = 28; the 31st is 31x16 = 496; and the 127th is 127x64 = 8128.
In base 10, the digital root of a triangular number is always 1, 3, 6, or 9. Hence every triangular number is either divisible by three or has a remainder of 1 when divided by nine:
- 1 = 9×0+1,
- 3 = 3×1,
- 6 = 3×2,
- 10 = 9×1+1,
- 15 = 3×5,
- 21 = 3×7,
- 28 = 9×3+1,
- 36 = 9×4,
- 45 = 9×5,
- 55 = 9×6+1,
- ...
- The digital root pattern, repeating every nine terms, is "1 3 6 1 6 3 1 9 9".
The inverse of the statement above is, however, not always true. For example, the digital root of 12, which is not a triangular number, is 3 and divisible by three.
If x is a triangular number, then ax+b is also a triangular number, given the following conditions are satisfied:
a=an odd square, b=(a-1)/8
Note that b will always be a triangular number, because 8Tn+1=(2n+1)2, which yields all the odd squares are revealed by multiplying a triangular number by 8 and adding 1, and the process for b given a is an odd square is the inverse of this operation.
The first several pairs of this form (not counting 1x+0) are: 9x+1, 25x+3, 49x+6, 81x+10, 121x+15, 169x+21,.... . Given x is equal to Tn, these formulas yield T3n+1, T5n+2, T7n+3, T9n+4, and so on.
The sum of the reciprocals of all the triangular numbers is:
This can be shown by using the basic sum of a telescoping series:
Two other interesting formulas regarding triangular numbers are:
and
both of which can easily be established either by looking at dot patterns (see above) or with some simple algebra.
In 1796, German mathematician and scientist Carl Friedrich Gauss discovered that every positive integer is representable as a sum of at most three triangular numbers, writing in his diary his famous words, "EΥΡHKA! num = Δ + Δ + Δ" Note that this theorem does not imply that the triangular numbers are different (as in the case of 20=10+10), nor that a solution with three nonzero triangular numbers must exist. This is a special case of Fermat's Polygonal Number Theorem.
The largest triangular number of the form 2k-1 is 4095, see Ramanujan–Nagell equation.
Wacław Franciszek Sierpiński posed the question as to the existence of four distinct triangular numbers in geometric progression. It was conjectured by Polish mathematician Kazimierz Szymiczek to be impossible. This conjecture was proven by Fang and Chen in 2007.[1][2]
Triangular roots and tests for triangular numbers
By analogy with the square root of x, one can define the (positive) triangular root of x as the number n such that Tn = x:[3]
An integer x is triangular if and only if 8x + 1 is a square. Equivalently, if the positive triangular root n of x is an integer, then x is the nth triangular number.[3]
See also
- 1 + 2 + 3 + 4 + …
- Metcalfe's law, that the complexity of communication between a group of people grows with the number of pairs of people, a triangular number.
- Miraculous Draught of Fish, an episode from the Gospels involving the triangular number 153; the triangular form of this number was thought by Saint Augustine to be important in interpreting this passage.[4]
- Pentagonal number
- Hexagonal number
Notes
- ^ Chen, Fang: Triangular numbers in geometric progression
- ^ Fang: Nonexistence of a geometric progression that contains four triangular numbers
- ^ a b Euler, Leonhard; Lagrange, Joseph Louis (1810), Elements of Algebra, 1 (2nd ed.), J. Johnson and Co., pp. 332–335
- ^ Owen, O. T. (1988), "One Hundred and Fifty Three Fishes", Expository Times 100: 52–54, doi:10.1177/001452468810000204.